FCNAgent class

Description

FCNAgent クラスのエージェントは，ファンダメンタル分析（F），チャート分析（C），正規ノイズ（N）の加重平均として予想リターン，および予想価格を算出する [CI2002]．次に，将来の予想価格と現在の価格を比較し，それらの大小関係に応じて買い注文／売り注文をだす．

以下に，FCNAgent の性質をまとめる．

ほぼ 100% 売り注文 or 買い注文をだす．
注文量は常に１単位のみ．
通常１つの銘柄のみを取引する．
予想リターンはエージェントの保有する資産（現金，株式）の数量に依存しない．

Model

エージェント $i$ はある単一の銘柄 $s$ のみを取引する．ある時点 $t$ における銘柄 $s$ の市場価格を $p_t$，ファンダメンタル価格を $v_t$ と記す（本稿では銘柄を表す添字 $s$ を省略する）．エージェントは銘柄 $s$ の期待リターンをファンダメンタル項 $F^i_t$ とテクニカル項 $C^i_t$ の組み合わせにノイズ項 $N^i_t$ を加えた荷重平均として見積もる．

$\hat{r}^i_t = \frac{1}{w_F^i + w_C^i + w_N^i} (w_F^i F^i_t + w_C^i C^i_t + w_N^i N^i_t)$

ここで，$w_F^i,~w_C^i,~w_N^i \ge 0$ は各項への重みである．

ファンダメンタル分析は現在の市場価格が将来的に理論価格へ接近するという期待に基づく．したがって，$F^i_t$ は理論価格 $v_t$ と市場価格 $p_t$ の乖離から

$F^i_t = \frac{1}{\tau^i} \ln(v_t / p_t)$

で与えられる．ここで，$\tau^i$ はエージェントの時間窓長である．

他方で，テクニカル分析は現在の価格推移の傾向が将来的にも継続するという期待に基づく．したがって，$C^i_t$ は過去 $\tau^i$ 期間にわたる市場価格の変化の時系列から

$C^i_t = \frac{1}{\tau^i} \sum_{j=0}^{\tau^i-1} \ln \frac{ p_{t-j} }{ p_{t-j-1} } = \frac{1}{\tau^i} \ln(p_t / p_{t - \tau^i})$

で与えられる．

最後に，ノイズ項は平均 $0$，分散 $(\sigma_N^i)^2$ の正規分布に従う．

$N^i_t \sim \mathcal{N}(0,~\sigma_N^i)$

期待リターン $\hat{r}^i_t$ より，現時点 $t$ で予想した将来の時点 $t + \tau^i$ の期待価格は次式で与えられる．

$\hat{p}^i_t = p_t \exp(\hat{r}^i_t \tau^i)$

この予想価格と現在の価格を比較して，注文を決定する．注文の決定（注文価格，売り買いの別）には 2 つの戦略がある．

Fixed margin trading

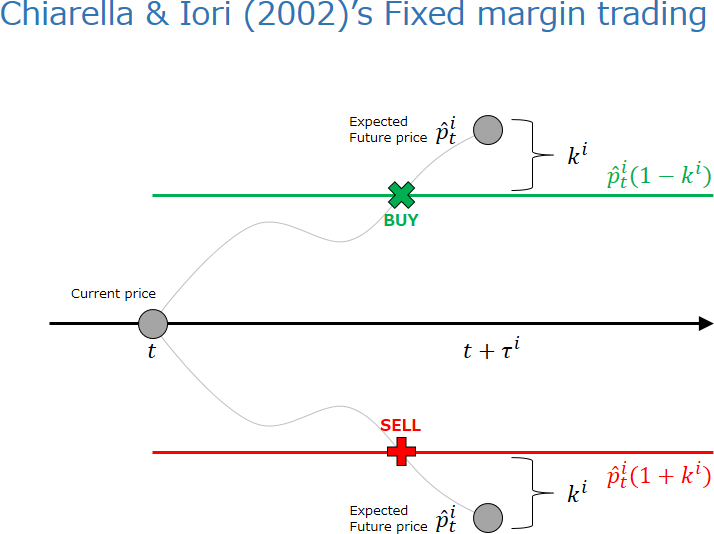
本記事で固定マージンと呼ぶ注文戦略を説明する（下記の図）．エージェントはあるマージン $k^i \in [0,1]$ をもつ．もし将来的な価格の上昇を予想するならば（$\hat{p}^i_t > p_t$），1 単位の買い注文を次の価格において出す．

$\hat{p}^i_t\,(1 - k^i)$

他方，もし価格の下落を予想するならば（$\hat{p}^i_t < p_t$），1 単位の売り注文を次の価格において出す．

$\hat{p}^i_t\,(1 + k^i)$

この戦略を図に示した．図では，価格の上昇を予想する場合と下落を予想する場合が同時に描かれている．

上昇を予想する場合（図上半分），$t + \tau^i$ での予想価格よりも割合 $k^i$ だけ安い価格で買い注文をだす．この注文は，市場価格が $t + \tau^i$ で予想価格に至るとすれば，それまでのいずれかの時点（図中，緑の×）で約定することが期待される．そして，$t + \tau^i$ の時点でこの約定により入手した資産を売り払うことで（ポジションを閉じる），価格差から利益をえることができる（安く買い高く売る）．

他方，価格の下落を予想する場合（図下半分），予想価格よりも割合 $k^i$ だけ高い価格で売り注文をだす．この注文は，市場価格が $t + \tau^i$ で予想価格に至るとすれば，それまでのいずれかの時点（図中，赤の＋）で約定することが期待される．そして，$t + \tau^i$ の時点でこの約定により手放した資産を買い戻すことで（ポジションを閉じる），価格差から利益をえることができる（高く売り安く買う）．

small

Gaussian margin trading

本記事で正規乱数マージンと呼ぶ注文戦略を説明する（下記の図）．エージェントはあるマージン $k^i > 0$ をもつ（$k^i$ の意味が変わっていることに注意）．エージェントは予想価格 $\hat{p}^i_t$ の周りで正規乱数

$\varepsilon^i_t \sim \mathcal{N}(0, k^i)$

を生成し，次の価格において注文をだす．

$\hat{p}^i_t + \varepsilon^i_t$

ただし，売り買いの別は以下とする．

$\hat{p}^i_t + \varepsilon^i_t < \hat{p}^i_t$ ならば「買い」
$\hat{p}^i_t + \varepsilon^i_t > \hat{p}^i_t$ ならば「売り」

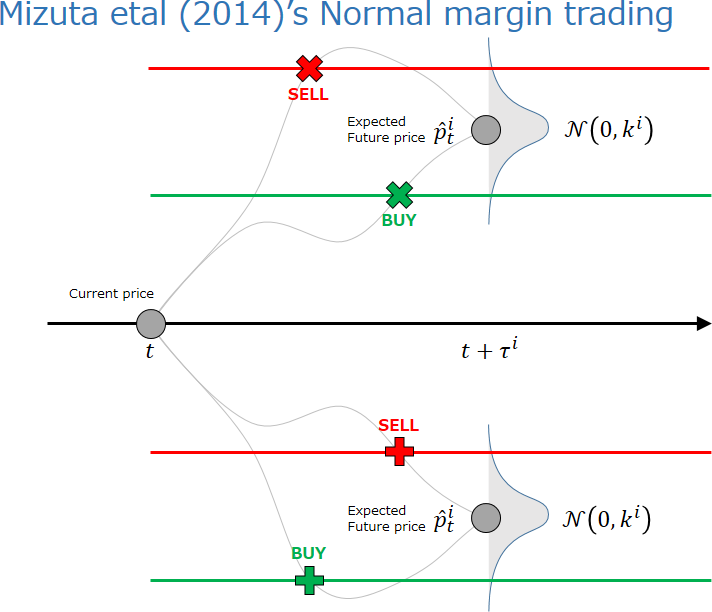
この戦略を図に示した．図では，価格の上昇を予想する場合と下落を予想する場合，さらに $\varepsilon^i_t$ が正の場合と負の場合（全 4 ケース）が同時に描かれている．基本的な原理は固定マージンと同じである．とくに，「上昇かつ負」および「下落かつ正」の場合は，固定マージンの説明がそのまま当てはまる．ここでは残りケースを説明する．

正規乱数マージンでは，予想価格の周辺ではランダムウォーク的な振る舞いが観察されるという仮定の上で，注文を決定する．

「上昇かつ正」の場合（図上半分），予想価格より高い価格で売り注文をだす．この注文は，市場価格が $t + \tau^i$ で予想価格に至るとしても，予想を超えて上昇しなければ約定しない．もし約定しなければ，$t + \tau^i$ でキャンセルされるので，利益も損益もない．他方，それまでのいずれかの時点（図中，赤の×）で約定したとすれば，$t + \tau^i$ でこの資産を買い戻すことで，利益をえられる（高く売り安く買う）．

他方，「下落かつ負」の場合（図下半分），予想価格より低い価格で買い注文をだす．この注文は，市場価格が $t + \tau^i$ で予想価格に至るとしても，予想を超えて下落しなければ約定しない．もし約定しなければ，$t + \tau^i$ でキャンセルされるので，利益も損益もない．他方，それまでのいずれかの時点（図中，緑の＋）で約定したとすれば，$t + \tau^i$ でこの資産を売り払うことで，利益をえられる（安く買い高く売る）．

small

Note: Impact on orderbooks

固定マージンと正規乱数マージンの違いは，とりわけ板の状態に影響を及ぼす．典型的には，正規乱数マージンのほうが，

最良気配値の価格差（スプレッド）が狭く，
仲値付近にも注文が十分に残る．

他方，固定マージンでは板が疎らになり，第２最良気配値が価格の離れた場所に出現しやすい．結果として，最良気配値の約定が仲値を大きく変化させるなどの副作用がみられる．

Parameters

	JSON keyword	Field variable
$w_F^i$	`fundamentalWeight`	`fundamentalWeight`	ファンダメンタル分析荷重
$w_C^i$	`chartWeight`	`chartWeight`	チャート分析荷重
$w_N^i$	`noiseWeight`	`noiseWeight`	正規ノイズ荷重
$\sigma^i$	`noiseScale`	`noiseScale`	正規ノイズの標準偏差
$\tau^i$	`timeWindowSize`	`timeWindowSize`	時間窓長
$k^i$	`orderMargin`	`orderMargin`	注文の価格幅
	`marginType`	`marginType`	注文の戦略 `fixed` or `normal`

Inherited parameters

Agent class : markets, cashAmount, assetVolumes

Complete JSON example

"My-FCNAgent": {
    "class": "FCNAgent",
    "numAgents": 100,

    "MEMO": "Agent class",
    "markets": ["Market-A"],
    "assetVolumes": 0,
    "cashAmount": 0,

    "MEMO": "FCNAgent class",
    "fundamentalWeight": 1.5,
    "chartWeight": 1.5,
    "noiseWeight": 1.5,
    "noiseScale": 0.1,
    "timeWindowSize": [10, 100],
    "orderMargin": 0.1
}

Parameter setup from JSON

fundamentalWeight

Class: plham.agent.FCNAgent
JSON key: fundamentalWeight
JSON value: Double >=0

エージェント $i$ のフィールド fundamentalWeight の値 $w_F^i$ は指数乱数から標本抽出される．指数分布はその期待値に対応する１つのパラメータ $\lambda_F$ をもつ． JSON ファイルでは，エージェントに関する記述のうち，fundamentalWeight キーワードにより $\lambda_F$ の値を指定できる．例）

{  "fundamentalWeight": 1.5  }

chartWeight

Class: plham.agent.FCNAgent
JSON key: chartWeight
JSON value: Double >= 0

エージェント $i$ のフィールド chartWeight の値 $w_C^i$ は指数乱数から標本抽出される．指数分布はその期待値に対応する１つのパラメータ $\lambda_C$ をもつ． JSON ファイルでは，エージェントに関する記述のうち，chartWeight キーワードにより $\lambda_C$ の値を指定できる．例）

{  "chartWeight": 1.5  }

noiseWeight

Class: plham.agent.FCNAgent
JSON key: noiseWeight
JSON value: Double >= 0

エージェント $i$ のフィールド noiseWeight の値 $w_N^i$ は指数乱数から標本抽出される．指数分布はその期待値に対応する１つのパラメータ $\lambda_N$ をもつ． JSON ファイルでは，エージェントに関する記述のうち，noiseWeight キーワードにより $\lambda_N$ の値を指定できる．例）

{  "noiseWeight": 1.5  }

noiseScale

Class: plham.agent.FCNAgent
JSON key: noiseScale
JSON value: Double >= 0

エージェント $i$ のフィールド noiseScale の値 $\sigma^i$ は，JSON ファイルのエージェントに関する記述のうち，noiseScale キーワードにより直接指定できる（乱数なし）．例）

{  "noiseScale": 0.1  }

timeWindowSize

Class: plham.agent.FCNAgent
JSON key: timeWindowSize
JSON value: [min:Long, max:Long] ... min > 0, max > 0

エージェント $i$ のフィールド timeWindowSize の値 $\tau^i$ は一様乱数から標本抽出される．一様乱数はその下限と上限に対応する２つのパラメータ $\tau_\min$，$\tau_\max$ をもつ． JSON ファイルでは，エージェントに関する記述のうち，timeWindowSize キーワードにより $\tau_\min$，$\tau_\max$ の値を指定できる．例）

{  "timeWindowSize": [10, 100]  }

orderMargin

Class: plham.agent.FCNAgent
JSON key: orderMargin
JSON value: Double >= 0

エージェント $i$ のフィールド orderMargin の値 $k^i$ は，JSON ファイルのエージェントに関する記述のうち，orderMargin キーワードにより直接指定できる（乱数なし）．例）

{  "orderMargin": 0.1 }

marginType

Class: plham.agent.FCNAgent
JSON key: marginType
JSON value: String, fixed or normal

エージェント $i$ の注文戦略を指定する．固定マージン戦略（fixed）か，正規乱数マージン戦略（normal）を指定できる．例）

{  "marginType": "normal"  }

Fields & Methods

特筆すべきフィールドやメソッドをもたない．

References

[CI2002] Carl Chiarella & Giulia Iori (2002) A simulation analysis of the microstructure of double auction markets. Quantitative Finance, vol.5, no.2, pp.346–353.

FCNAgent -- Plham documentation