OptionMain UseCases 01
本記事では,tutorial/OptionMain で解説したプログラムを使い,実際にシミュレーションを行う.
シミュレーションの実行とグラフ化
問.1
プログラムをコンパイル・実行し,ボラティリティ・サーフェイスをグラフ化せよ.
解説
コンパイルは以下の手順で行う.
$ x10c++ samples/Option/OptionMain.x10
コンパイルに成功すると実行ファイル a.out が生成される.
今回実行するシミュレーションでは以下のエージェントを用いる. 以下では,Frijns (2010) 型のエージェントをまとめて,オプション FCN エージェントと呼ぶ.
"UnderFCNAgents" |
原資産のみを取引する FCNAgent (Chiarella & Iori 2002) |
"UnderRandomAgents" |
原資産のみを取引するランダムエージェント (Chiarella & Iori 2002) |
"FundamentalistOptionAgents" |
オプションを取引するファンダメンタリスト (Frijns 2010) |
"ChartistOptionAgents" |
オプションを取引するチャーチスト (Frijns 2010) |
"NoiseOptionAgents" |
オプションを取引するノイズエージェント (Frijns 2010) |
"OptionRandomAgents" |
オプションを取引するランダムエージェント (Chiarella & Iori 2002) |
次に,シミュレーションを実行し,ボラティリティ・サーフェイスのグラフを描画する(出力ファイルは output.png; このとき,2 次元平面のヒートマップ output-2d.png も一緒に生成される).
$ ./a.out samples/Option/config.json >output.dat
$ Rscript samples/Option/volsurface.R output.dat output.png
以下に output.png を示す.
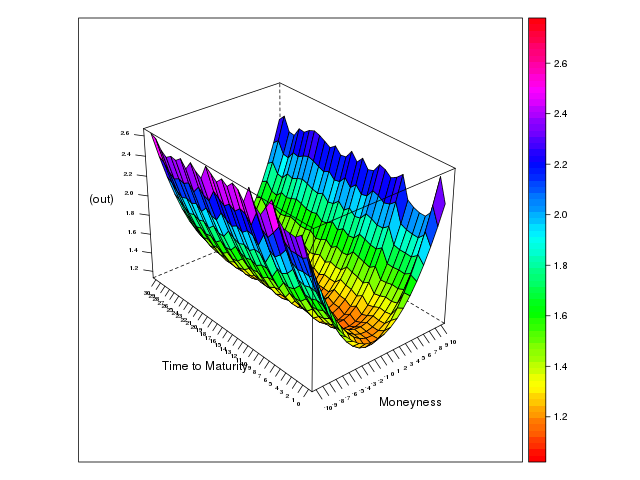
原資産 FCN エージェント,オプション FCN エージェントの場合
上記の図 output.png では,ボラティリティ・サーフェイスはスマイル形状を示している. この図では Tompkins (2001) の手法を用いて,シミュレーションデータを多項式で近似している.
原資産 ランダム,オプション FCN エージェントの場合
問.2
原資産を取引する FCNAgent がランダム的(ランダムウォーク)である場合を検証せよ. プログラムをコンパイル・実行し,ボラティリティ・サーフェイスをグラフ化せよ.
解説
このために,config.json の "simulation"/"agents" を以下に書き換える.
"simulation": {
"agents": ["UnderRandomAgents", "FundamentalistOptionAgents", "ChartistOptionAgents", "NoiseOptionAgents"]
}
シミュレーションを実行し,ボラティリティ・サーフェイスのグラフを描画する.
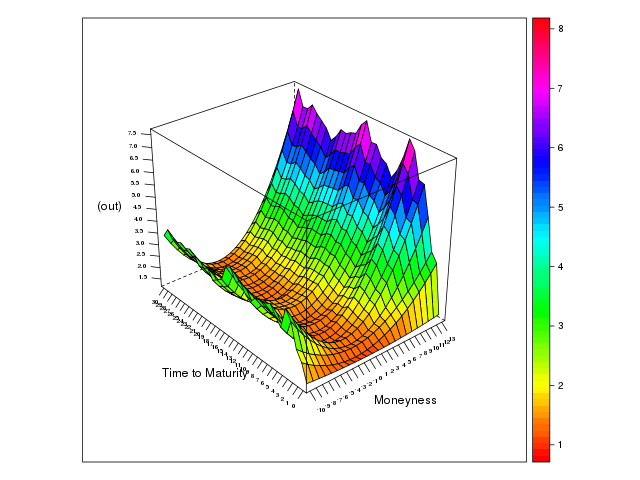
図から,原資産トレーダがランダム的である場合にもスマイル形状が確認できる. ただし,この結果の場合,スマイルが非対称になっている.
原資産 FCN エージェント,オプション ランダムの場合
問.3
オプションを取引するトレーダがランダム的(ランダムウォーク)である場合を検証せよ. プログラムをコンパイル・実行し,ボラティリティ・サーフェイスをグラフ化せよ.
解説
このために,config.json の "simulation"/"agents" を以下に書き換える.
"simulation": {
"agents": ["UnderFCNAgents", "OptionRandomAgents"]
}
ここで,"OptionRandomAgents" は Chiarella & Iori (2002) 型のエージェントである(Frijns (2001) 型はボラティリティをランダムに予想するだけで,ランダムウォークになる保証はないため).
シミュレーションを実行し,ボラティリティ・サーフェイスのグラフを描画する.
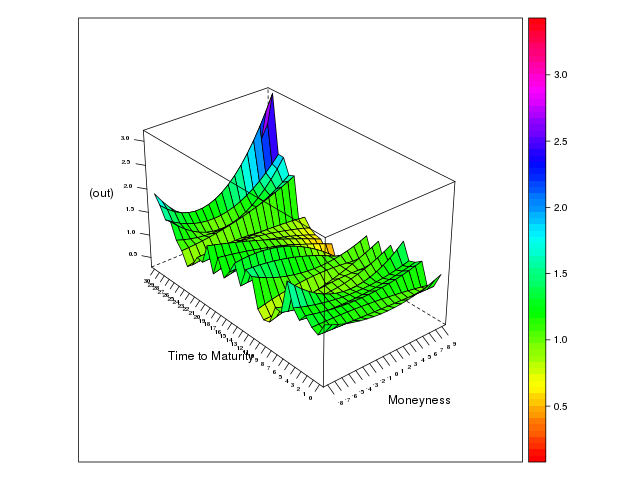
図から,オプショントレーダがノイズ的である場合には,スマイル形状が消失していることが確認できる. サーフェイスは平たく,また試行によって異なった様相を示す. インプライド・ボラティリティは Black-Scholes モデルを用いて算出されるが,この結果は Black-Scholes モデルが価格のランダムウォークと定数ボラティリティを仮定したモデルであることに関係していると思われる. 今回のように価格がランダムウォークする場合にはインプライド・ボラティリティも平均的に定数になったと考えられる.
原資産 ランダム,オプション ランダムの場合
問.4
原資産を取引するトレーダも,オプションを取引するトレーダも,両方ランダム的である場合を検証せよ. プログラムをコンパイル・実行し,ボラティリティ・サーフェイスをグラフ化せよ.
解説
このために,config.json の "simulation"/"agents" を以下に書き換える.
"simulation": {
"agents": ["UnderRandomAgents", "OptionRandomAgents"]
}
シミュレーションを実行し,ボラティリティ・サーフェイスのグラフを描画する.
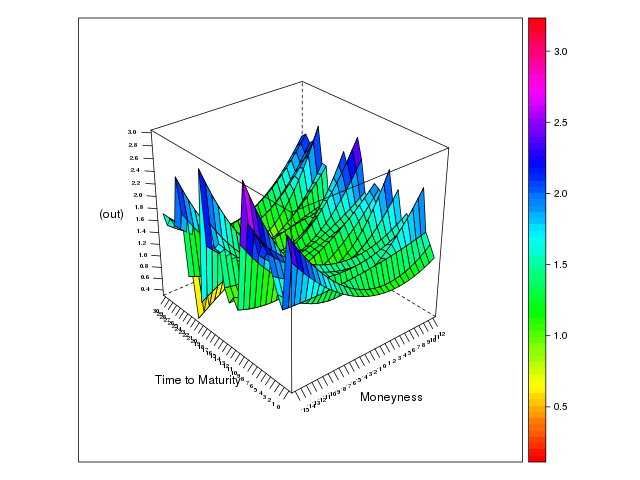
図から,両方のトレーダがランダム的である場合には,スマイル形状が消失していることが確認できる. サーフェイスは凹凸が激しく,また試行によって異なった様相を示す. この結果は,問.3 に比べて,サーフェイスの乱雑さが目立つ.